Professora Evelyn: Equações biquadradas

Equações biquadradas

"

Uma equação biquadrada é toda aquela que possui a forma:

$ax^4+bx^2+c=0$

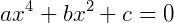
Note que uma equação biquadrada é muito semelhante com uma equação do segundo grau (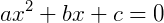 $ax^2+bx+c=0$ ). Esta semelhança será crucial para que possamos solucionar uma equação biquadrada.

Para encontrarmos raízes para este tipo de equação é necessário fazer uma troca de variáveis. Como já vimos que ela é muito semelhante a uma equação quadrática comum, podemos transformá-la em uma. Veja abaixo um exemplo genérico:

$ax^4+bx^2+c=0$

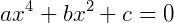
Se igualarmos 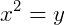$x^2=y$ , por exemplo, podemos reescrever a nossa expressão acimada forma de uma equação quadrática, ou seja:

$ay^2+by+c=0$

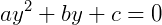
Então:

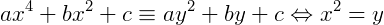
$ax^4+bx^2+c\equiv ay^2+by+c\Leftrightarrow x^2=y$

Com esta substituição, nos basta resolver a equação do segundo grau encontrada e depois disso, substituir o valor de 𝑦 na igualdade 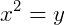$x^2=y$ .

Exemplo 1) Vamos resolver a equação abaixo:

$x^4-6x^2+9=0$

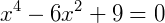
Antes, faremos a substituição 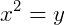$x^2=y$ e, reescrevendo temos:

$y^2-6y+9=0$

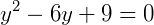
Resolvendo:

$\Delta=b^2-4ac$

$\Delta=(-6)^2-4\cdot 1\cdot 9$

$\Delta=36-36=0$

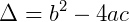
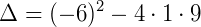
Continuando:

$y=\frac{-b\pm\sqrt{\Delta}}{2a}$

$y=\frac{-(-6)\pm\sqrt{0}}{2\cdot 1}=\frac{6}{2}=3$

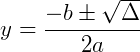
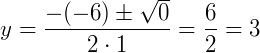
Encontrado o valor de 𝑦, substituímos então na igualdade:

$x^2=y$

$x^2=3$

$x=\pm\sqrt{3}$

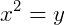
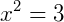
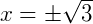
Então, encontramos o valor 𝑥 para a equação biquadrada, vamos conferir:

$x^4-6x^2+9=0$

$(\pm\sqrt{3})^4-6(\pm\sqrt{3})^2+0=0$

$9-18+9=0$

$0=0$

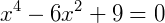
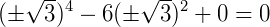
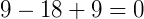
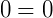
Exemplo 2) Vamos resolver a equação abaixo:

$x^4-5x^2+6=0$

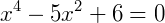
Substituição 𝑥² = 𝑦:

$y^2-5y+6=0$

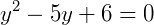
Resolvendo:

$\Delta=b^2-4ac$

$\Delta=(-5)^2-4\cdot 1\cdot 6$

$\Delta=25-24=1$

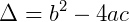
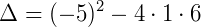
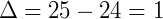
Continuando:

$y=\frac{-b\pm\sqrt{\Delta}}{2a}$

$y=\frac{-(-5)\pm\sqrt{1}}{2\cdot 1}\Rightarrow\begin{cases}y_1=\frac{5+1}{2}=\frac{6}{2}=3\\y_2=\frac{5-1}{2}=\frac{4}{2}=2\end{cases}$

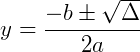
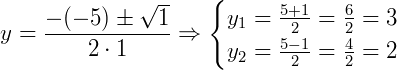
Encontramos agora dois valores para 𝑦, o que também resulta dois valores para 𝑥:

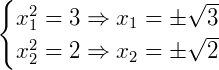
$\begin{cases}x_1^2=3\Rightarrow x_1=\pm\sqrt{3}\\x_2^2=2\Rightarrow x_2=\pm\sqrt{2}\end{cases}$

Substituindo na equação biquadrada obtemos:

$x^4-5x^2+6=0$

$(\pm\sqrt{3})^4-5(\pm\sqrt{3})^2+6=0$

$9-15+6=0$

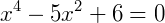
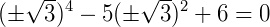
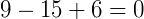
Ou,

$x^4-5x^2+6=0$

$(\pm\sqrt{2})^4-5(\pm\sqrt{2})^2+6=0$

$4-10+6=0$

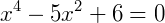
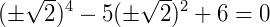
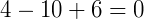
Referências Bibliográficas:

DANTE, Luiz Roberto. Matemática: Contexto e Aplicações. Volume 3. São Paulo: Editora Ática, 2011.

DEMANDA, Franklin D; WAITS, Bert K.; FOLEY, Gregory D.; KENNEDY, Daniel. Pré Calculo. São Paulo: Pearson, 2013.

The post Equações biquadradas appeared first on InfoEscola.

InfoEscola http://bit.ly/2JniqsW
Publicado primeiro em https://www.infoescola.com"

Nenhum comentário:

Postar um comentário

Assinar: Postar comentários (Atom)