Em matemática, podemos representar conjuntos, subconjuntos e soluções de equações pela notação de intervalo. Intervalo significa que o conjunto possui cada número real entre dois extremos indicados, seja numericamente ou geometricamente. Não é possível representar subconjuntos ou conjuntos que não sejam reais (ou contidos nos reais) pela notação de intervalo.
Vamos, por exemplo, dizer que o conjunto A é um subconjunto dos números naturais e que será representado por:

Note que qualquer elemento de A pertence ao conjunto dos naturais, porém é um absurdo dizer que nos naturais existem números entre 1 e 2, ou seja, em ℕ não existe o número 1,5 , por exemplo. Então, neste caso, dizemos que o conjunto A é vazio. E será representado por:

Logo não é correto dizer que A = [1,2]. A não é um subconjunto dos números reais, então nem todos os números possíveis estão no intervalo quaisquer números naturais, ou inteiros ou racionais.
Mas, se A fosse um subconjunto dos reais, poderíamos dizer que:
![A = \{x \in \mathbb{R} : 1 \leq x \leq 2\} = [1, 2]](https://www.infoescola.com/wp-content/plugins/latex/cache/tex_0ccf951e0ff485cf5a76d3186ea95354.gif)
O que geometricamente representamos:
Notações
1. Dizemos que um intervalo é aberto quando seus extremos não estão incluídos. Exemplo:
![]a, b[ = \{x \in \mathbb{R} : a < x <b\}](https://www.infoescola.com/wp-content/plugins/latex/cache/tex_f6078ed6105f0e65b005f3cec456ccb3.gif)
Geometricamente representamos por uma bolinha branca indicando o elemento não incluído:
O intervalo também é aberto quando indicamos apenas um dos extremos e o outro pode ser uma infinidade de elementos à direita ( ) ou à esquerda (
) ou à esquerda ( ). Ou seja:
). Ou seja:
![]a, +\infty[ = \{x \in \mathbb{R} : x > a\}](https://www.infoescola.com/wp-content/plugins/latex/cache/tex_e29f0c4024dd570bd34647b7775cbeac.gif)
![]-\infty, a[ = \{x \in \mathbb{R} : x < a\}](https://www.infoescola.com/wp-content/plugins/latex/cache/tex_f8570d6fe4b582878c654447736a7200.gif)
Toda ocasião em que um extremo for uma infinidade de elementos, este sempre será um extremo aberto.
2. Um intervalo fechado é aquele em que seus extremos são incluídos:
![[a, b]= \{x \in \mathbb{R} : a \leq x \leq b\}](https://www.infoescola.com/wp-content/plugins/latex/cache/tex_54fbbe22c6649a7471a4390afa693748.gif)
Na reta, o elemento incluído será uma bolinha preta:
3. Dizemos que um intervalo é semiaberto ou semifechado quando um de seus extremos são incluídos, ou seja:

![]a, b] = \{x \in \mathbb{R} : a < x \leq b\}](https://www.infoescola.com/wp-content/plugins/latex/cache/tex_e6dc002e7be420fadd432acc4fa6ff36.gif)
E também com extremos ao infinito:

![]-\infty, a] = \{x \in \mathbb{R} : x \leq a\}](https://www.infoescola.com/wp-content/plugins/latex/cache/tex_b305810913923adece4236132ce4c2d9.gif)
Podemos também assumir que, se um intervalo é um subconjunto dos números reais, é possível realizar algumas operações entre intervalos, tais como união e interseção de intervalos. Supondo que tenhamos dois intervalos: [a, b] e [c, d] e que d > c > b > a.
A união dos intervalos será dada por:
![[a, b] \cup [c, d] = \{x \in \mathbb{R} : a \leq x \leq b \text{ ou } c \leq x \leq d\}](https://www.infoescola.com/wp-content/plugins/latex/cache/tex_9915b7f04447fe895f52c3307d39d612.gif)
E geometricamente representamos:
E a sua interseção é vazia, pois não existem elementos comuns em ambos os intervalos:
![[a, b] \cap [c, d] = \emptyset](https://www.infoescola.com/wp-content/plugins/latex/cache/tex_2127589de453c3172ae9d64854675ad5.gif)
Vamos tomar um exemplo com valores. Supondo os intervalos [1,5] e [2,7]. A sua união será:
![[1, 5] \cup [2, 7] = [1, 7] = \{x \in \mathbb{R} : 1 \leq x \leq 7\}](https://www.infoescola.com/wp-content/plugins/latex/cache/tex_f07fee047c6f0e3f6033401c8ec9956d.gif)
Se representarmos na reta, vemos que seus elementos estão ligados linearmente:
Então a sua união será a “soma” de todos os elementos de seus intervalos, resultando em um intervalo único de 1 a 7. Porém, a sua interseção será dada por:
![[1, 5] \cap [2, 7] = [2, 5] = \{x \in \mathbb{R} : 2 \leq x \leq 5\}](https://www.infoescola.com/wp-content/plugins/latex/cache/tex_521c9e19cfca6d433e1217afdfbde6de.gif)
Geometricamente vemos que existe um intervalo entre eles que é composto pelos elementos que são comuns em ambos, no caso, o intervalo [2,5], veja:
Concluindo: Intervalos serão sempre subconjuntos dos números reais, o que nos garante a validade de todas as propriedades e operações da teoria dos conjuntos. A representação geométrica de um intervalo é muito importante pois podemos observar o comportamento dos intervalos, facilitando a sua classificação e as suas possíveis operações.
Referências Bibliográficas:
LIMA, Elon Lages. Um Curso de Análise: Volume 1. Rio de Janeiro: IMPA, 2017.
GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.
The post Intervalo appeared first on InfoEscola.
InfoEscola https://ift.tt/2KOupgE
Publicado primeiro em https://www.infoescola.com"
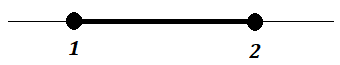


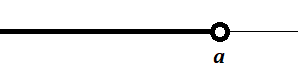

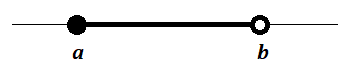

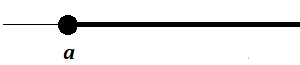




Nenhum comentário:
Postar um comentário