Professora Evelyn: Funções matemáticas

O estudo de funções matemáticas é, de fato, um dos mais importantes e historicamente relevantes para a construção de toda a ciência. Neste caso, vamos abordar um pouco mais o formalismo matemático para definir o que vem a ser uma de suas estruturas mais importantes.

Definição 1: Uma função f (ou aplicação) é uma relação entre dois conjuntos quaisquer, A e B, e uma regra que permite associar a cada elemento de A um único elemento de B. Isto quer dizer, em linguagem matemática, que:

f : A → B

Lê-se f de A em B

Chamamos o conjunto A de Domínio da função e B o Contradomínio. É importante atentar-se à diferença entre função f, que é a própria função, e f(x) que é o valor da função em um determinado ponto x no seu domínio. Sendo assim, podemos dizer que para cada valor de x que pertence ao domínio A, existe um único valor y (ou f(x)) que pertença ao contradomínio B. Usualmente escrevemos:

$y = f(x) \longleftrightarrow \{x \in A\text{ e }y \in B\}$

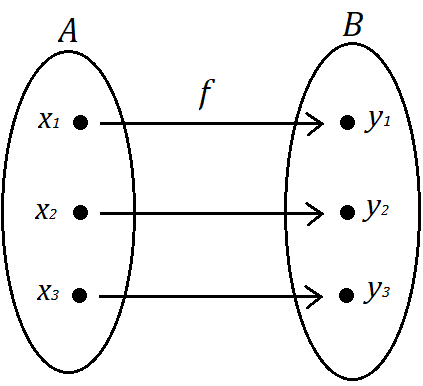
Podemos representar uma função através de um diagrama, como no exemplo abaixo:

Gráfico de uma função

Seja f : A → B uma função, dizemos que o seu gráfico é o subconjunto G_f , formado por todos os pares ordenados (x, y) ou (x, f(x)) no produto cartesiano (ou relação binária) A x B. Então:

$G_f = \{(x, y) \in AxB : y = f(x)\}$ ou $G_f = \{(x, f(x) : x \in A\text{ e }y \in B\}$

Lê-se: O gráfico de f é o conjunto formado pelos pares ordenados (x,y) pertencentes ao produto AxB, tal que y=f(x).

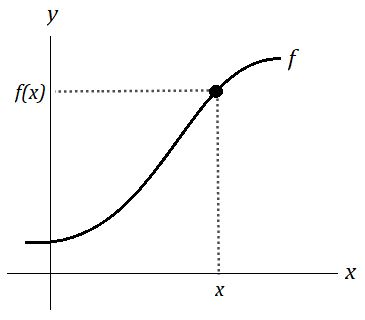
Então, seja uma função f : A → B onde y=f(x), dizemos que o seu gráfico deve ser o lugar geométrico composto por todos os pontos (x, f(x)).Tratamos x como uma variável independente e y a variável dependente, ou seja, y é função de x:

Domínio, contradomínio e imagem

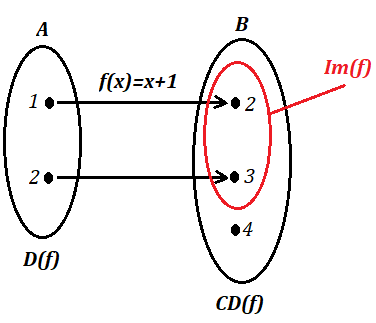
Vamos analisar a função definida por: f : A → B, f(x) = x+1, sendo A = {1,2} e B = {2,3,4}. Veja abaixo o diagrama:

Explicando de uma forma simplificada as definições de domínio, contradomínio e imagem, podemos dizer que:

Domínio: de onde partem as flechas;
Contradomínio: os elementos que as flechas podem acertar;
Imagem: os elementos foram atingidos pelas flechas.

Em linguagem formal, dizemos:

Domínio: D(f) = A
Contradomínio: CD(f) = B
Imagem: Im(f) = {2, 3}

Funções de uma variável real

Quando dizemos que a função está definida no conjunto dos números reais então é usual representa-la por f de uma variável real e com domínio em $\mathbb{R}$ . Sendo assim:

$f : \mathbb{R} \longrightarrow \mathbb{R}, f(x) = y$

E o seu gráfico será definido por todos os pontos, tais que:

$G_f = \{(x, y) \in \mathbb{R}^2 : y = f(x)\}$

Seja a função $f : \mathbb{R} \lingrightarrow \mathbb{R}$ onde $f(x) = x^3$ . Vamos determinar o seu domínio, o contradomínio, sua imagem e esboçar o seu gráfico.

Ora, o seu domínio está definido nos reais, pois para qualquer valor de x teremos sempre um correspondente em y nesta função. O mesmo ocorrerá com o seu contradomínio, pois qualquer de y em função de x estará contido no conjunto dos números reais. Então dizemos que:

$D(f) = CD(f) = \mathbb{R}$

Para esboçarmos o gráfico da função, num primeiro momento, é mais fácil estipular alguns valores de x para sabermos qual será o seu correspondente y. Podemos construir uma pequena tabela, como no exemplo abaixo, iniciando de -3 a 3:

x	y=f(x)
-3	-27
-2	-8
-1	-1
0	0
1	1
2	8
3	27

Obs: Estes valores de x foram escolhidos arbitrariamente, mas podem ser testados com quaisquer outros, desde que os mesmos sejam números reais. O gráfico da função deverá então estará definido, segundo a definição, no conjunto:

$G_f = \{(x, y) \in \mathbb^2 : y = x^3\}$

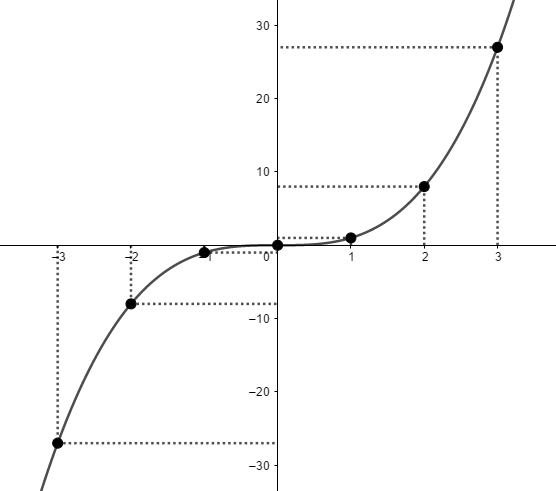
E o seu esboço será, com x indo de -3 a 3:

Abaixo temos alguns exemplos de funções e seus respectivos domínios escritos também com outras notações.

FUNÇÃO	DOMÍNIO
$f(x) = \frac{1}{x}$	$D(f) = \{x \in \mathbb{R} : x \neq 0\}$ ou $D(f) = \mathbb{R} - \{0\}$ ou $D(f) = \mathbb{R}^{*}$
$f(x) = \sqrt{x}$	$D(f) = \{x \in \mathbb{R} : x \geq 0\}$ ou $D(f) = \mathbb{R}_{+}$ ou $D(f) = \[0, +\infty\[$
$f(x) = \frac{1}{\sqrt{x}}$	$D(f) = \{x \in \mathbb{R} : x > 0\}$ ou $D(f) = \]0, +\infty\[$ ou $D(f) = \mathbb{R}_{+}^{*}$
$f(x) = log x$	$D(f) = \{x \in \mathbb{R} : x > 0\}$ ou $D(f) = \]0, +\infty\[$ ou $D(f) = \mathbb{R}_{+}^{*}$