É chamada função afim toda função polinomial do primeiro grau. Formalmente escrevemos que:
Uma função  é uma função afim quando existem dois números reais a e b tais que satisfaçam a seguinte condição,
é uma função afim quando existem dois números reais a e b tais que satisfaçam a seguinte condição,  e
e  temos:
temos:

Onde:
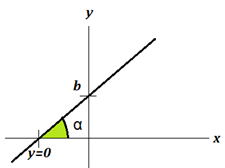
- a é o coeficiente angular do gráfico de f
- b é o coeficiente linear, ou o ponto de intersecção com o eixo y
- x é a variável independente.
Podemos determinar o valor de a pela tangente do ângulo  formado pela interseção do gráfico da função com o eixo x, ou seja:
formado pela interseção do gráfico da função com o eixo x, ou seja:

Basicamente, o gráfico de uma função afim será sempre uma reta. Os fatores que vão determinar a sua posição no plano são os coeficientes linear e angular, particulares de cada função. Vamos apresentar alguns problemas que envolvem funções afim:
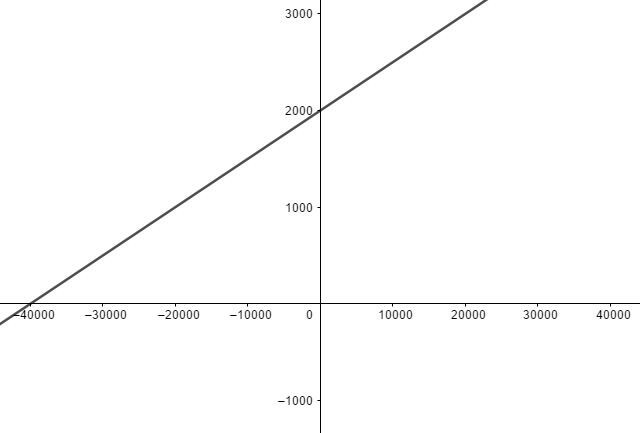
Exemplo 1) Supondo que você é um vendedor, cujo salário mensal é de R$ 2.000,00. Porém, a cada produto vendido você ganha uma comissão de 5%, ou 0,05 vezes o valor do produto. A função que descreverá, em função do valor vendido durante o mês é do tipo afim, e será descrita pela lei:
f(x) = 0,05x + 2000
Existem ainda alguns casos particulares das funções afim. Estes são:
Função identidade
Seja uma função  definida por f(x) = x. Então, neste caso se a = 1 e b = 0, o gráfico de uma função identidade é chamada de bissetriz dos quadrantes impares, que passam pelo 1º e 3º quadrante e na origem do eixo cartesiano (0, 0).
definida por f(x) = x. Então, neste caso se a = 1 e b = 0, o gráfico de uma função identidade é chamada de bissetriz dos quadrantes impares, que passam pelo 1º e 3º quadrante e na origem do eixo cartesiano (0, 0).
Função constante
Uma função  é dita constante quando f(x) = b, logo a = 0. Seu gráfico será sempre uma reta paralela ao eixo x e que intercepta o eixo y num ponto b.
é dita constante quando f(x) = b, logo a = 0. Seu gráfico será sempre uma reta paralela ao eixo x e que intercepta o eixo y num ponto b.
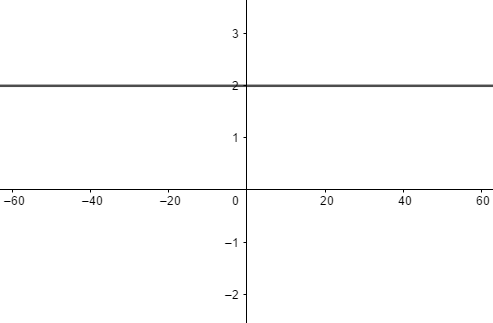
Por exemplo, seja a função f(x) = 2, o seu gráfico será:
Função linear
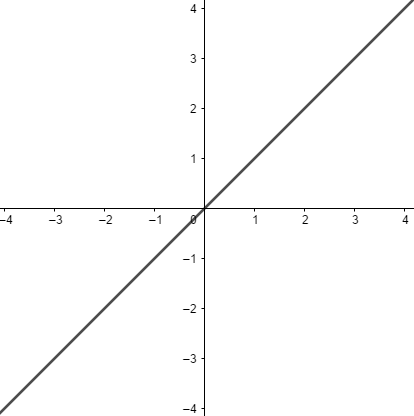
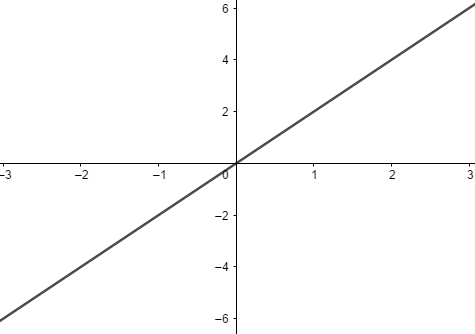
Uma função  é dita constante quando f(x) = ax, logo b = 0. Seu gráfico será sempre uma reta paralela que intercepta a origem do eixo cartesiano. Por exemplo, a função f(x) = 2x terá a sua representação gráfica dada por:
é dita constante quando f(x) = ax, logo b = 0. Seu gráfico será sempre uma reta paralela que intercepta a origem do eixo cartesiano. Por exemplo, a função f(x) = 2x terá a sua representação gráfica dada por:
Translação da função identidade
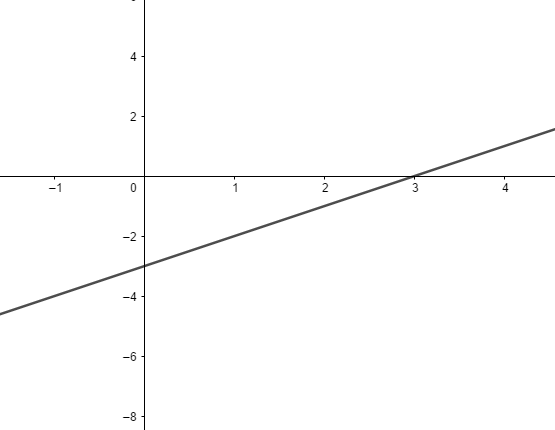
Se tomarmos a função identidade e acrescentarmos à ela um coeficiente linear e mantendo o seu coeficiente angular igual a 1, ocorrerá a translação da reta. A função será definida por f(x) = x+b sendo a = 1 e  . Por exemplo, f(x)= x-3:
. Por exemplo, f(x)= x-3:
Características das Funções Afim
- Uma função afim é crescente se a > 0;
- Uma função afim é decrescente se a < 0;
Referências Bibliográficas:
LIMA, Elon Lages. Um Curso de Análise: Volume 1. Rio de Janeiro: IMPA, 2017.
GUIDORIZZI, Hamilton L. Um Curso de Cálculo: Volume 1. Rio de Janeiro: Editora LTC, 2001.
The post Função afim appeared first on InfoEscola.
InfoEscola https://ift.tt/2LfZACu
Publicado primeiro em https://www.infoescola.com"
Nenhum comentário:
Postar um comentário